Hyperbolic Functions
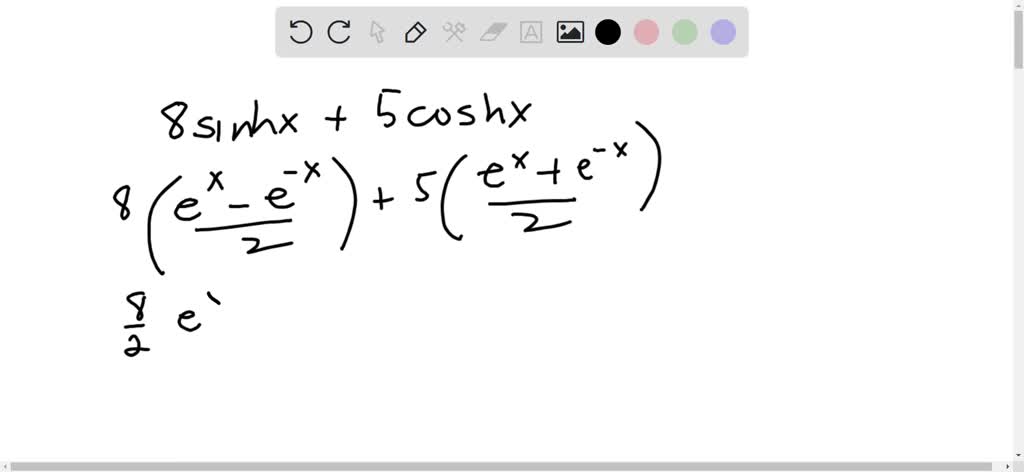
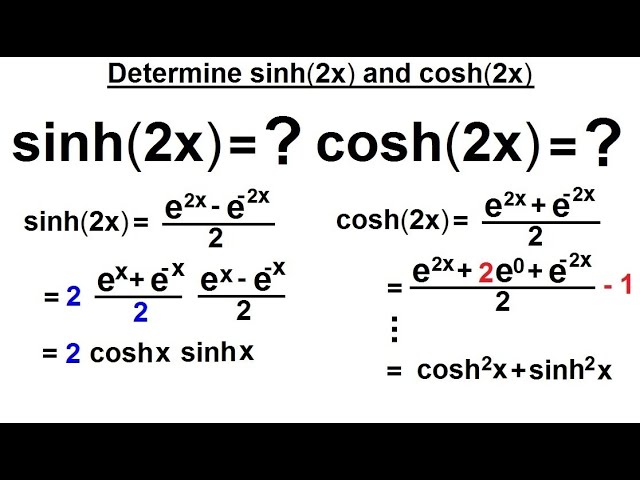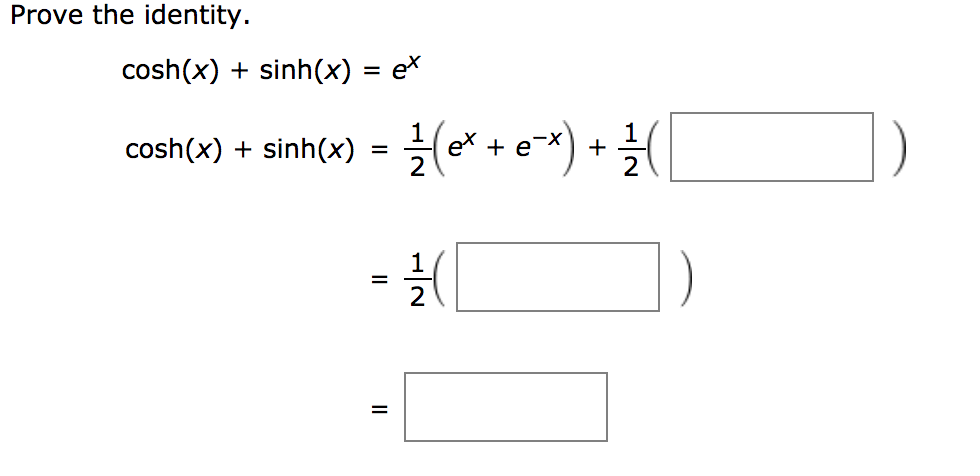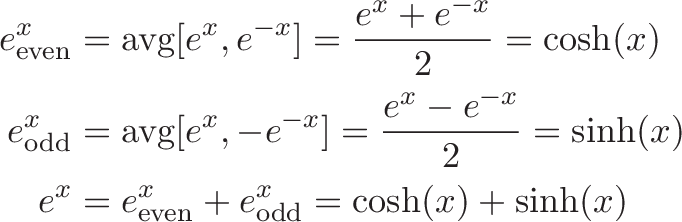The hyperbolic sine of u is defined as \sinh u = \frac{1}{2} ( e ^u - e ^{-u}). The hyperbolic cosine of u is defined as \cosh u = \frac{1}{2} ( e ^
Prove that cosh x - sinh x = e-x - Stumbling Robot
Calculus 2: Hyperbolic Functions (13 of 57) Determine sinh(2x)=? and cosh(2x)=? - YouTube
Solved The basic hypergeometric functions are defined as - | Chegg.com
Solved Prove the identity. Cosh(x) + sinh(x) = e^ - X | Chegg.com
7.6 The Hyperbolic Functions
Hyperbolic functions - Wikipedia
Cosh(x) function is the average of e x and e − x Hyperbolic functions... | Download Scientific Diagram
Solved The hyperbolic cosine and sine functions (see | Chegg.com
Hyperbolic functions - Wikipedia
Evaluate the integral. ∫_0^(ln 2) 2e^-x cosh x dx | Quizlet
Solved The functions sinh x and cosh x are defined as | Chegg.com
Prove a Property of Hyperbolic Functions: sinh(x+y)=sinh(x)cosh(y)+cosh(x)sinh(y) - YouTube
Hyperbolic functions - Wikipedia
SOLVED: Euler'formula; which says cos 0 + i sin 0 where i satisfies the equation 12 -1. Recall also that the hyperbolic cosine and hyperbolic sine functions are defined as +e-r and
Hyperbolic functions. - ppt download
Hyperbolic Functions
Funciones hiperbólicas - Wikiversidad
Hyperbolic functions - Wikipedia
7.6 The Hyperbolic Functions
Hyperbolic Trigonometric Functions | Brilliant Math & Science Wiki
Solved 3. Using the Euler identity, show that hyperbolic | Chegg.com
SOLVED:Write 8 sinhx+5 coshx in terms of e^x and e^-x.
Intuitive Guide to Hyperbolic Functions – BetterExplained
File:Division e^x-1; cosh(x+arcosh(2))-2.png - Wikimedia Commons
Solved Since = 1 2 and cosh(x) = { (e® tec) +-0 sinh(z) = | Chegg.com
Hyperbolic functions - Wikipedia
![An elementary course of infinitesimal calculus . = cosh X 1sinh a; .(2). We notice that cosh a;, like cos a;, is an even functionof X ] i.e. it is unaltered](https://c8.alamy.com/comp/2CDC892/an-elementary-course-of-infinitesimal-calculus-=-cosh-x-1sinh-a-2-we-notice-that-cosh-a-like-cos-a-is-an-even-functionof-x-ie-it-is-unaltered-by-writing-x-for-a-whilst-sinh-xlike-sin-x-is-an-odd-function-ie-the-function-is-unalteredin-absolute-value-but-reversed-in-sign-by-the-same-substitu-tion-of-a-for-x-the-continuity-of-cosh-x-and-sinh-x-follows-from-thatof-e-and-e-bj-a-theorem-of-art-13-the-figure-on-thenext-page-shews-the-curves-ye-y-=-e-together-with-the-curves-y-=-cosh-x-y-=-sinh-x-which-are-derived-from-them-by-taking-half-the-sum-andhalf-th-2CDC892.jpg "An elementary course of infinitesimal calculus . = cosh X 1sinh a; .(2). We notice that cosh a;, like cos a;, is an even functionof X ] i.e. it is unaltered")